Welcome to my homepage !
Table of Contents
Hello \(!\)
My name is Manh Tien NGUYEN.
I am a PhD student in Mathematics at Université Libre de Bruxelles and Aix-Marseille Université.
My supervisors are Joel Fine and Julien Keller.
For the last 3 years, I studied harmonic maps and minimal surfaces, mostly in(to) the
hyperbolic space.
On your right is a surface of the Euclidean 3-space. It looks quite minimal and it grows on my lemon tree.

Here are a few more minimal surfaces, this time in 4D. They are all surfaces of revolution.
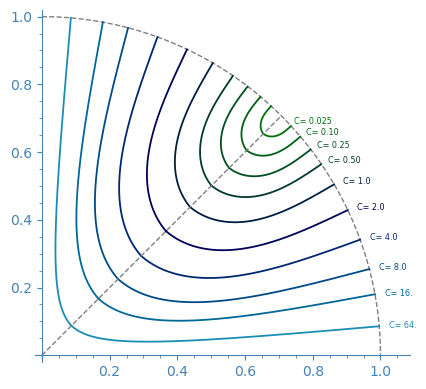
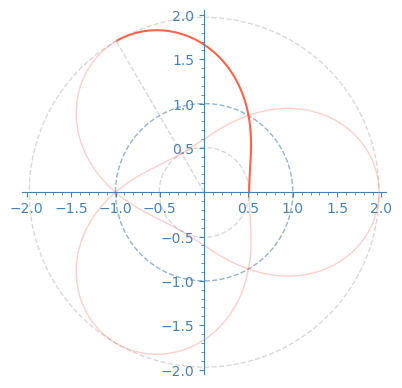
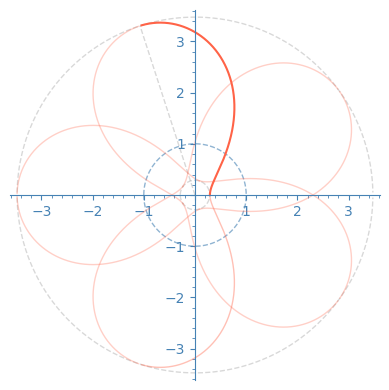
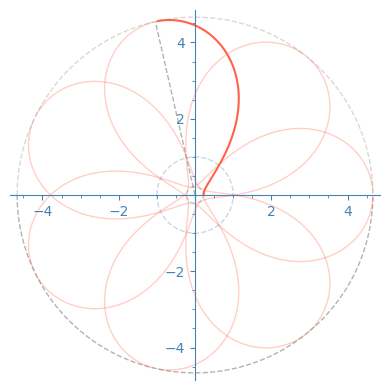
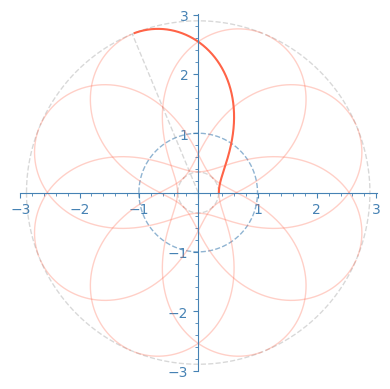
The rotation used here is given by simultaneously changing each complex coordinate of \(\mathbb{C}^2\) by an opposite phase.
I claim that when you rotate these curves,
- those in the left figure will form minimal annuli in the hyperbolic four-space.
- those in the 4 figures on the right will become minimal tori of the round four-sphere.
Links
- A GUI editor for commutative diagram with
tikzcd, also originally hosted by the author. - If you prefer
xypic, use this one. Source code.