Divisors, Picard group and Kodaira embedding theorem

1. Divisors and Picard group
- 1.1. Holomorphic line bundles and first Chern class
- 1.2. Divisors, line bundles and sheaves
  - 1.2.1. From divisors to Picard group
  - 1.2.2. The corresponding line bundle of $ \mathcal{O}(Y) $
2. Example: Projective space
3. Blowing-up
- 3.1. Blowing-up
4. Kodaira vanishing theorem
5. The traditional proof of Kodaira embedding theorem
6. An analytic proof by Donaldson

The PDF version of this page can be downloaded by replacing html in the its address by pdf. For example /html/sheaf-cohomology.html should become /pdf/sheaf-cohomology.pdf.

1 Divisors and Picard group

1.1 Holomorphic line bundles and first Chern class

A complex line bundle is a 2 dimensional vector bundle with a complex structure on each fiber, i.e. each change of coordinates $ g_{ij}: U_j\cap U_i \times \mathbb{R}^2 \longrightarrow U_i\cap U_j\times\mathbb{R}^2 $ is $ i $-linear, i.e. $ g_{ij} $ can be represented by a function $ U_{i}\cap U_j \longrightarrow \mathbb{C} $.

A holomorphic line bundle is a complex line bundle that is also a complex manifold with the projection being holomorphic. In the same notation, the $ g_{ij} $ are now holomorphic functions.

A hermitian metric on a line bundle $ L $ is a positive sesquilinear form on each fiber. To define the Chern form of $ L $, let $ U $ be an open set of $ X $ over which $ L $ is trivialized and $ s_x $ is a holomorphic section of $ L $ over $ U $ that is non-vanishing, then one defines \[ \omega_{L,h} = \frac{1}{2\pi i}\partial \bar \partial \log |s|_h^2 \] which is independant of $ s $ since the ratio of two different $ s $ is in $ \mathcal{O}^*(U) $.

A Chern form is a real (1,1) form.

The set of isomorphic class of holomorphic line bundle is in one-to-one correspondance to $ H^1(X,\mathcal{O}_X^*) $

The proof of this fact is straightforward, but it is worth to remark that this result convinces us that the natural mapping $ \check{H}^1(\mathcal{U},X) \longrightarrow \check{H}^1(\mathcal{V},X) $ where $ \mathcal{U} $ is a finer open covering than $ \mathcal{V} $ is injective, since a line bundle is completely defined by one set of change of coordinates $ (g_{ij}) $.

Now the Chern class of a holomorphic line bundle is the class of $ \omega_{L,h} $ in $ H^2(X,\mathbb{Z}) $, which turns out to be independent of $ h $ and is in fact lies in the image of $ H^2(X,\mathbb{Z}) \longrightarrow H^2(X,\mathbb{R}) = H^2(X, \mathbb{Z})\otimes_{\mathbb{Z}}\mathbb{R} $. In fact, the class of $ \omega_{L,h} $ can be defined using the following exact sequence: \[ 0 \longrightarrow \mathbb{Z} \longrightarrow \mathcal{O}_X \longrightarrow \mathcal{O}_X^* \longrightarrow 0 \] where the injective arrow is the multiplication by $ i2\pi$ and the surjective one is exponential. The Chern map is in fact $ H^1(X,\mathcal{O}^*_X) \longrightarrow H^2(X,\mathbb{Z}) $. To prove this, one uses a double complex whose horizontal is the de Rham resolution and vertical is the Čech resolution and diagram chasing.

1.2 Divisors, line bundles and sheaves

A holomorphic line bundle is the same as a locally free $ \mathcal{O}_X $-module of rank 1.
An isomorphic class of line bundles is the same as a locally free isomorphic sheaf of $ \mathcal{O}_X $-module of rank 1.

1.2.1 From divisors to Picard group

A divisor is a formal sum of irreducible hypersurface, which can also be intepreted as an element of $ \check{H}^0(X,K_X^*/\mathcal{O}_X^*) $, which gives a mapping $ Div(X) \longrightarrow \check{H}^0(X,K_X^*/\mathcal{O}_X^*) $ with principal divisors being exactly sent to elements of $ K_X^*/\mathcal{O}_X^* $ coming from $ K_X^* $. multiplicative).

Since the following sequence \[ 0 \longrightarrow \mathcal{O}_X^* \longrightarrow K_X^* \longrightarrow K_X^*/O_X^* \longrightarrow 0 \] is exact, one has an application $\mathcal{O}:\ Div(X) = H^0(X, K_X^*/\mathcal{O}_X^*) \longrightarrow H^1(X, \mathcal{O}_X^*) = Pic(X) $. The kernel of $ \mathcal{O} $ corresponds to the the space of principal divisors. It is however worth having details of the application $\mathcal{O} $.

Let $ D = (U_i,f_i)\in Div(X) $ where $ f_i $ are meromorphic function on $ U_i $ with $ f_i/f_j\in \mathcal{O}_X^* $, then $ \mathcal{O}(D) $ is defined as following: \[ \mathcal{O}(D) (U_i) = f_i^{-1}\mathcal{O}_X(U_i) \]. Note that if $ D $ is effective, i.e. $ f_i\in \mathcal{O}_X(U_i) $ then $ \mathcal{O(D)} $ is the sheaf of holomorphic functions vanishing on $ D $.

To resume, here are some basic consequence of the above discussion: If $ D $ is effective then

If $ D $ is effective then $ H^0(X, \mathcal{O}(D) \ne 0 $.
If $ D $ is effective then $ \mathcal{O}(-D) $ is the sheaf of holomorphic function vanishing on $ D $. Therefore $ \mathcal{O}(-D) $ can be viewed as a ideal subsheaf of $ K_X $ and one has the following exact sequence: \[ 0 \longrightarrow \mathcal{O}(-D) \longrightarrow \mathcal{O}_X \longrightarrow \mathcal{O_D} \longrightarrow 0 \] where $ \mathcal{O}_D $ is the sheaf of "regular functions" on $ D $.
If $ L $ is a holomorphic line bundle and $ 0\ne s\in H^0(X,L) $ then $ \mathcal{O}(Z(s)) \equiv L $
If $ D $ is effective then $ \mathcal{O}(D) $ has a non-zero global section, for example section $ 1 = (U_i, f_i) $

1.2.2 The corresponding line bundle of $ \mathcal{O}(Y) $

Let $ Y $ be a hypersurface of $ X $, then the line bundle $ \mathcal{O}(Y) $ is isomorphic to $ \mathcal{N}_{Y,X} $ the normal line bundle of $ Y $ in $ X $.

By consequence, $ K_Y = \restr{(K_X\otimes \mathcal{O}(Y))}{Y} $.

2 Example: Projective space

2.1 $ \mathcal{O}(d) $ and its sections

Let's have some examples for the point of view discussed above, starting with the torsion sheaves $ \mathcal{O}(d) $.

The sheaf $ \mathcal{O}(-1) $, called tautological sheaf, is an invertible sheaf on $ \mathbb{P}^n_{\mathbb{C}} $ such that the fiber over $ l\in \mathbb{P}^n_{\mathbb{C}} $ of the corresponding line bundle is $ l $ itself. Let $ l=[x_0:\dots:x_n] \ in U_i $ then a point in $ l $ is of form $ t_i[\frac{x_0}{x_i}:,\dots:\frac{x_n}{x_i}] $ with coordinates in $ U_i $ being $ t_i $. So the change of coordinates from chart $ U_i $ to $ U_j $ is, since $ \frac{t_j}{x_j} = \frac{t_i}{x_i} $: \[ g_{ji} = \frac{x_i}{x_j} \] One notes by $ \mathcal{O}(1) $ the dual of $ \mathcal{O}(-1) $ and $ \mathcal{O}(d) = \mathcal{O}(1)^{\otimes d} $ and $ \mathcal{O}(-d)=\mathcal{O}(-1)^{\otimes d} $

Now if an invertible sheaf $ \mathcal{L} $ with $ \mathcal{L}(U_i) = \frac{1}{f_i}\mathcal{O}_X(U_i) $, the change of coordinates of the corresponding line bundle from chart $ U_i $ to $ U_j $ is $ g_{ji} = \frac{f_j}{f_i} $. So for $ \mathcal{O}(1) $, one has $ \frac{f_j}{f_i} = \frac{x_j}{x_i} $, i.e. there exists a linear combination $ A $ of $ x_0,\dots, x_n $ such that $ f_i = \frac{A}{x_i} $ is a holomorphic function correponding to the 1-section viewed in chart $ U_i $. As presented in the previous section, $ \mathcal{O}(1) $ is the associated line bundle of a hyperplane defined by the equation $ A = 0 $.

Similarly, $ \mathcal{O}(d) $ is the associated line bundle of a hypersurface $ A_d $ defined by a homogenous equation of degree $ d $, and $ \mathcal{O}(d) $ is the line bundle associated to the sheaf of holomorphic functions vanishing on $ A_d $.

2.2 Line bundles and maps to projective space, Veronese embedding

A linearly independent family $ s_0,\dots, s_N $ of global sections of a holomorphic line bundle $ L $ defines a holomorphic map $X\setminus Bs((s_i)) \longrightarrow \mathbb{P}^N_{\mathbb{C}} $ where $ Bs((s_i)) $ is the set of basepoints of $(s_i)$ where all the sections $ s_i $ vanish.

The global sections of $ \mathcal{O}(d) $ over $ \mathbb{P}^n_{\mathbb{C}} $ are $ H^0(\mathbb{P}^n_{\mathbb{C}}, \mathcal{O}(d) = \mathbb{C}[z_0,\dots,z_n]_d $ the vector space of homogenous polynomial of degree $ d $. The corresponding projective map is in fact a embedding, called Veronese embedding.

2.3 Canonical bundle and Euler sequence

\[ K_{\mathbb{P}^n_{\mathbb{C}} = \mathcal{O}(-n-1)} \]

\[ 0 \longrightarrow \mathcal{O} \longrightarrow \mathcal{O}(1)^{\oplus n} \longrightarrow \mathcal{T}_{\mathbb{P}_{\mathbb{C}}^n} \longrightarrow 0 \]

3 Blowing-up

3.1 Blowing-up

Let $ X $ be a complex manifold, $ x\in X $ and $ \pi:\ \hat X \longrightarrow X $ is the blow-up of $ X $ at $ x $ and $ E $ be the corresponding exceptional divisor, then \[ K_{\hat X} = \pi^* K_X \otimes \mathcal{O}((n-1)E). \] As a consequence, $ \restr{\mathcal{O}(E)}{E} = \mathcal{O}(-1) $ where $ \mathcal{O}(-1) $ is the tautologic sheaf over $ E = \mathbb{P}^{n-1}_{\mathbb{C}} $.

The appearance of the number $ n-1 $ is natural and can be explained as follow. First note that

in $ \hat X\setminus E $, there is no difference between $ K_{\hat X} $ and $ K_X $.
$ \pi_* $ send every tangent vector of $ E $ to the tangent vector $ 0 $ at $ x\in X $,
the pull-back $ \pi^* \omega $ of an $ n $-form on $X $ always vanishes on $ E $ therefore cannot generate $ K_{\hat X} $.

Our correction of this should be dividing $ \pi^* \omega $ by $ f^k $ where $ f $ is the equation defining $ E $ in $ \hat X $, i.e. tensoring $ \pi^* K_X $ by an appropriate multiple of $ \mathcal{O}(E) $ depending on the order of vanishing of $ \pi^* \omega $ at $ E $, which we claim to be $ n-1 $.

Here is the argument I used to convince myself: this vanishing order is that of the ratio of $ \pi^* \omega $ and a non-zero $n $-form (says the standard in the base formed by $ n-1 $ tangent vectors $ e^E_i $ of $ E $ and the normal vector $ v $ of $ E $ in $ X $), i.e. the vanishing order of $ \pi^*\omega(e^E_i, v) $. Each $ e^E_i$ plugged into $ \pi^*\omega $ adds one order of vanishing resulting in $ n-1 $.

Here is the argument I would use to convince others: WLOG, suppose that $ X = \mathbb{C}^n $ and $ x=0 $, then $ \hat X $ can be seen as a subset of $ \mathbb{C}^n\times \mathbb{P}^{n-1} $ with the coordinates in each chart $ U_i = \left\{(x_1, \dots, x_n,[p_1:\dots:p_n]):\ p_i\ne 0\right\}$ being $ (\frac{p_1}{p_i},\dots,\frac{p_n}{p_i},\zeta_i) $ with $ z_k = \frac{p_k}{p_i}\zeta_i $. The map $ \pi $ is given in local coordinates as \[ (\frac{p_1}{p_i},\dots,\frac{p_n}{p_i},\zeta_i) \mapsto (\frac{p_1}{p_i}\zeta_i, \dots \zeta_i, \dots \frac{p_n}{p_i}\zeta_i) \] The pull-back of $ \omega $ is \[ d(\frac{p_1}{p_i}\zeta_i)\wedge\dots\wedge d\zeta_i \wedge \dots\wedge d(\frac{p_n}{p_i}\zeta_i) = \zeta_i^{n-1}d(\frac{p_1}{p_i})\wedge\dots\wedge d\zeta_i\wedge\dots\wedge d(\frac{p_n}{p_i}) \] which vanishes with order $ n-1 $.

For the consequence, note that $ \mathcal{K}_E = \mathcal{O}(-n) = \restr{(K_{\hat X}\otimes \mathcal{O}(E))}{E} = \restr{(\pi^* K_{X}\otimes \mathcal{O}(nE))}{E} $, but $ \pi^* K_X $ is trivial over $ E $, therefore $ \restr{\mathcal{O}(E)}{E} = \mathcal{O}(-1) $.

4 Kodaira vanishing theorem

Let $ X $ be a compact complex manifold of dimension $ n $ and $ L $ is a positive holomorphic line bundle on $ X $, i.e. there exists a hermitian metric $ h $ on $ L $ such that the Chern form $ \omega_{L,h} $ is positive (i.e. a Kahler form). Then \[ H^q(X,\Omega_X^p \otimes \mathcal{L}) = 0 \quad\forall p+q >n. \] In particular, \[ H^i(X, K_X\otimes \mathcal{L}) = 0 \quad \forall i>0. \]

Since $ \mathcal{H}^{0,q}(E) \simeq H^q(X,\mathcal{E}) $ for all hermitian holomorphic vector bundle $ E $ with $ \mathcal{E} $ the corresponding sheaf of holomorphic sections. One needs to prove that all harmonic form in $ \mathcal{A}_X^{p,q}(L) $ vanishes for $ p+q>n $. This comes from the following two identities: Let $ \nabla $ be the Chern connection on $ L $ and $ \nabla = \nabla' + \nabla'' $ be its decomposition to $ (1,0) $ and $ (0,1) $ operators and $ \Delta_L' $ be the Laplacian corresponding to $ \nabla' $ then

$ \Delta_L = \Delta'_L + 2\pi[L,\Lambda] $ where $ L $ and $ \Lambda $ are Lefshetz operators.
$[L,\Lambda] = (k-n)Id_{\mathcal{A}^k_X}$

Therefore $ 0\leq(\alpha,\Delta'a)_{L^2} = 2\pi (n-k)(\alpha,\alpha)_{L^2}\leq 0 $

5 The traditional proof of Kodaira embedding theorem

Let $ X $ be a compact complex manifold with $ L $ a positive holomorphic line bundle on $ X $. Then $ L $ is generated by finitely many of its global sections and $ X $ can be embedded in a projective space $ \mathbb{C}\mathbb{P}^N $ with $ N $ sufficiently large.

The following approache is straight-forward: one shows that at every $ x\in X $, there is a global (holomorphic) section $ s_x $ of $ L^{\otimes m_x} $ such that $ s_x(x)\ne 0 $ then by compactness one can choose finitely many such sections and $ m_x $ which can be guaranteed to generate every germs at $ x $ of $ L^{\otimes m} $ with $ m=\max m_x $. That is one needs to prove that \[ H^0(X,\mathcal{L}^{\otimes m_x}) \twoheadrightarrow H^0({x}, \restr{\mathcal{L}^{\otimes m_x}}{x}) \] is surjective. Let $ \pi: \hat X \longrightarrow X $ be the blow-up of $ X $ at $ x $ and $ E = \pi^{-1}(x) $ be the corresponding exceptional divisor then one has

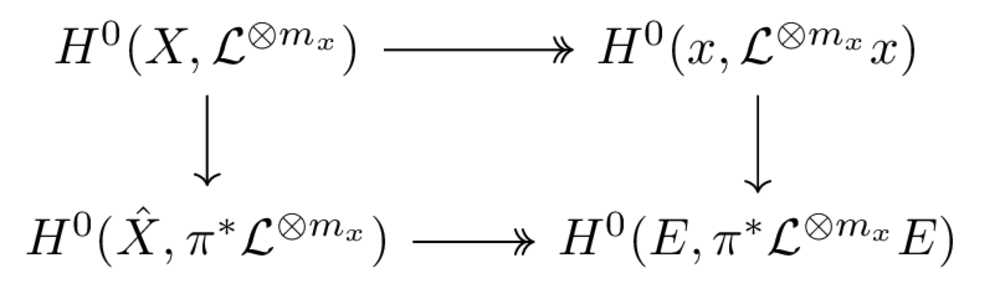
Figure 1: Insert caption [fig:kodaira-blowup]

where the vertical arrows are isomorphic (easy to see, maybe the right one needs Hartog). So one only needs to see that $H^0(\hat X,\pi^*\mathcal{L}^{\otimes m_x}) \twoheadrightarrow H^0(E,\restr{\pi^*\mathcal{L}^{\otimes m_x}}{E})$. Since $ E $ is a divisor of $ \hat X $, one has $ 0 \longrightarrow \mathcal{O}(E) \longrightarrow \mathcal{O}_{\hat X} \longrightarrow \mathcal{O}_E \longrightarrow 0 $ hence \[ 0 \longrightarrow \mathcal{O}(E)\otimes\pi^* \mathcal{L}^{\otimes m_x} \longrightarrow \pi^* \mathcal{L}^{\otimes m_x} \longrightarrow \restr{\pi^*\mathcal{L}^{\otimes m_x}}{E} \longrightarrow 0. \]

It remains to prove that $ H^1(\hat X, \mathcal{O}(E)\otimes\pi^* \mathcal{L}^{\otimes m_x}) $, or by thm:Kodaira-vanishing, that $ \mathcal{O}(E)\otimes\pi^* \mathcal{L}^{\otimes m_x}\otimes K_{\hat X}^{-1} = \mathcal{O}(-nE)\otimes\pi^* (\mathcal{L}^{\otimes m_x}\otimes K_X^{-1}) $ is positive, where we used the fact that $ K_{\hat X} = \pi^* K_X\otimes \mathcal{O}_{\hat X}((n-1)E) $.

Note that on $ \hat X \setminus E $, one can choose $ m_x $ large enough such that $ \mathcal{L}^{\otimes m_x}\otimes K_X^{-1}\times \mathcal{O}(-nE) $ is positive. It remains to observe $ E\subset \hat X $ which is in fact $ \mathbb{CP}^{n-1} $. But $ \restr{\mathcal{O}(-E)}{E} \equiv \mathcal{O}(1) $ is positive, which concludes the proof.